Course: Modeltheoretic Semantics and the Syntax-Semantics Interface
Eddy Ruys and Yoad Winter
Topics: entailment, model, the truth-conditionality criterion, compositionality, structural ambiguity, vaguenessConsider the sentence in (1).
For the personal angle of Barbara Partee see her reflections, or in a shorter version.
(2). The ability to draw such inferences is shared by
all speakers despite the fact that
words like "Tina", "tall" and "thin"
may mean different things
to different people in different occasions. For instance, you and I may
disagree on whether Tina is thin or not. Moreover, it is also possible
that we disagree on the identity of "Tina".
You may think that Tina in (1) is, say, Tina Turner,
and I may think that (1) speaks of Tina Charles.
However, we are quite unlikely to disagree on whether (2) is a sound conclusion
from (1). This uniform behaviour of entailment across speakers appears because
it is a relative notion:
if we are willing to accept (1) then
we must accept (2) as well, as a matter of language use.
We can describe the entailment (1)(2) informally by saying that
if sentence (1) is true then also (2) is true. Note that the converse does not
hold: if Tina is thin but not tall then (2) is true but (1) isn't. Hence
(2) does not entail (1).
What can be an explanation of these facts? This is a question that most semantic theories want to answer. In fact, many works in linguistic semantics are often concerned primarily with entailment relations and not with the more general notion of meaning. The reason is that it is not easy to define what people really mean when they talk about ``the meaning of a sentence''. Entailment, by contrast, is a relation between sentences of natural language about which speakers have in many cases solid and uniform intuitions. For this reason, we often loosely speak about the meaning of sentences, but actually refer only to their entailment potentials with respect to other sentences.
Modeltheoretic semantics tries to explain entailments by relating natural language expressions to certain abstract entities in a given structure, which is called a model. In technical terminology, we say that natural language expressions denote or refer to objects in the model. In every model there are two special entities that are called 1, or true, and 0, or false. These are the two truth values in the model. Sentences denote truth values, calculated in a way that the theory should specify. We try to explain entailment relations between sentences as relations between their possible truth values. The theory will be considered adequate only if it satisfies the following criterion.
entail sentence S
. Then whenever the theory
takes S to denote true,
it also takes S to denote true,
and vice versa.
Example 1: Let us illustrate a model-theoretic account of the entailment from (1) to (2). Assume that the model includes a non-empty set E of individuals and that the word Tina denotes a certain element tina' of this set. Assume further that the words tall and thin denote two subsets of E: tall' and thin'. These three objects are arbitrary denotations: there is no restriction on what element/subset of E they may be. By contrast, the denotations of and and is are defined systematically by:
tall' 
thin'
thin'
If you are familiar with philosophical or mathematical logic, all of this may sound very much alike. Indeed, the relations between linguistic semantics and traditional logic are very deep. However, there are at least two important differences between the two disciplines. First, linguistic semantics is only interested in natural languages spoken by humans. Logical semantics also concerns artificial languages like mathematical languages or computer languages. Second, logical theories, to the extent they are interested in natural language, are often only interested in what sentences in a language mean. Linguistic semantics also asks: how come sentences in human languages mean what they do? In other words: what are the relations between the sound and the form of a sentence and its meaning? There are many ways in which the sound and the form of a sentence can affect its meaning. Consequently, theories of language sounds (phonology) and language forms (syntax) are related to semantic theory in intricate ways.
In this course we concentrate on the relations between syntax and modeltheoretic semantics. Thus, we will study the question of how the structure of an expression affects the ways in which it is assigned a denotation. A principle that most versions of modeltheoretic semantics adopt is the following.
Example 2: Consider how we compositionally get to the truth value of sentence (1) based on the tentative structure as given in figure 1a.
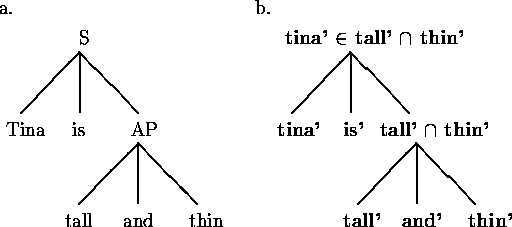
Figure 1: compositional meaning derivation
Syntactically,
this is not a very plausible structure, of course, but it is good enough to
demonstrate the idea of compositionality. The denotations of the lexical items
in the sentence are defined as in example 1. The denotation
of the adjective phrase
projecting tall and thin is determined by the denotation of its parts:
the intersection function 
and the sets 
and
. Also the denotation of the whole sentence is determined by
the denotation of its parts: 
, 
and 
. Given that the denotation is the membership
function, what we get is the truth value in (1').
Note a crucial aspect of this process: the denotation of a complex expression is only determined by the denotation of its parts. Given the structure in figure 1a, we cannot, for instance, define the denotation of the whole sentence directly on the basis of the denotation of the word tall. This is not one of the sentence's constituents. In order to compute the denotation of the sentence we must first compute the denotation of the complex predicate tall and thin. This hierarchical strategy is significantly restrictive: it does not tell us how exactly to derive the denotation of complex expressions, but it does tell us how this denotation cannot be derived given the syntactic structure.
A possible source of confusion is the status of formulae like (1'). Note that the formula itself is not the denotation of the sentence. The denotation of the sentence is a truth value, which is an object in the model. A formula like (1') is not a modeltheoretic object. It is only a recipe that indicates how the denotation of the sentence is defined as a function of its lexical items: for any choice of the denotations of Tina, tall and thin, (1') specifies what truth value the sentence is going to denote.
Compositionality helps in clarifying an important issue in linguistic theory: the phenomenon of structural ambiguity. Consider the following sentence:
(2).
There is however a common intuition that (3) entails (2), but only
under a particular
intention of the speaker. This intention can be made clear by putting
a comma intonation after the word tall. By contrast, the speaker
can use (3) correctly to describe a situation where
Tina is not thin. For instance, if I assert (1) you may react by (3) in order
to deny my assertion. As a response to my utterance of (1) you
may say something like:
``Come one, you must be wrong. Tina is not tall and thin, because even though she is indeed very tall, we all know that she is terribly fat''.Under this interpretation (3) does not entail (2) of course.
This intuition about the double nature of (3) is described by saying that (3) is an ambiguous sentence with two readings: one of them entails (2), the other does not. The striking thing about this kind of ambiguity is the ease with which it is described by all syntactic theories. Sentence (3) is analyzed as having two different syntactic structures, as roughly illustrated in figure 2.
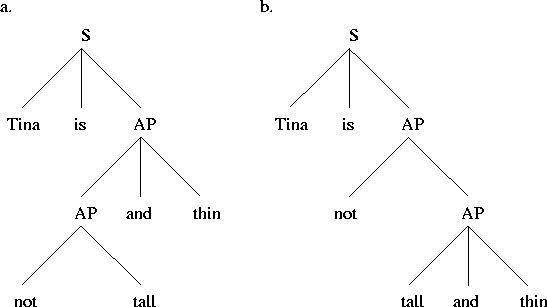
Figure 2: structural ambiguity
When a grammar generates in this way more than one structure for an
expression we say that the expression is treated as structurally
ambiguous. This syntactic ambiguity can be conceived of as an account of the
semantic ambiguity in (3). However, there is a gap in this account: why does
it follow that the structural ambiguity of (3) makes it also semantically
ambiguous? Compositionality provides the missing link. When the two structures
in figure 2
are compositionally interpreted, we immediately see that they
may have two different truth values. Concretely, assume that the denotation
of not in (3) is the complement function not', mapping any subset
A of E to its complement set: 
(the set of all the members of E that are not in A).
Under this assumption, the compositional interpretation of the two structures
in figure 2 is as illustrated in figure 3.
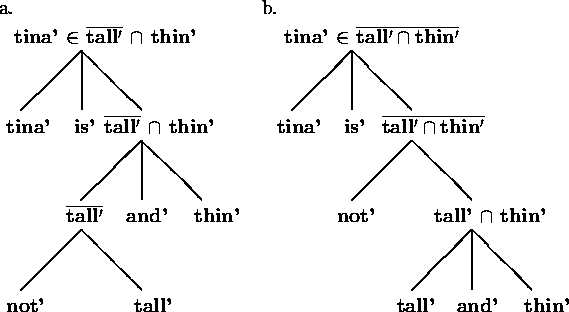
Figure 3: compositionality and ambiguity
Whenever the truth-value derived in figure 3a is true also the
truth-value assigned for (2) is true. Hence, this structure describes
the reading of (3) that entails (2). By contrast, the reading derived in
figure 3b does not entail (2): in case the element
is in the complement set 
it is not
necessarily in
the set , hence in such cases (2) may be assigned the truth-value
false.
We observe here an important property of compositional systems: the structure of a sentence corresponds directly to its entailment relations. Therefore, a structurally ambiguous sentence may have different truth values, hence different entailment relations, for its different structures. The entailment relations of a structure are fully specified. However, if a sentence has more than one structure, then it can happen that the entailment relations of the sentence are not fully specified, in accordance with the semantic ambiguity intuition.
It is important to distinguish the semantic-syntactic ambiguity of sentences like (3) from another type of semantic under-specification, which is called vagueness. For instance, a sentence like Tina walked does not entail the sentence Tina walked slowly. More generally, it underspecifies the manner of Tina's walk, as well as many other details about her and her walk. In practice, virtually all sentences are vague in this way, simply because we cannot expect one sentence to inform us about everything there is. In ambiguous sentences like (3) the intuition is quite different: we have the impression that (3) can entail sentence (2), but without further phonological clues it underspecifies whether this is indeed the case. In other words: the speaker can use (3) as if it entailed (2). In cases like (3) this ambiguity judgement is clear enough. However, it is often hard to judge whether sentences are ambiguous or just vague. In fact, the decision on this matter is rarely a purely pre-theoretical question and it often involves complex theoretical considerations, as we shall see later in this course.
Exercises
Tina is both tall and thin Tina is both blond or
tall and blond or thin
John is unhealthy. Why can't the kind of explanation
presented in class account for this entailment as well?
Give more examples of this sort.
Try to think of an addition to the theory that can account for such
entailments.